关键词: css css transform

关于此课程

这是一个UX设计师的课程。接触数据越多越来越习惯通过js来处理事情。

此课程按照简单到难的顺序一共有八个任务，由浅入深的带大家了解 Web 动效落地方法 。完成这八道题，你会掌握如下技能：

  • 熟练掌握 CSS transition 、transform 、animation 的用法 ;
  • 怎么从一份动效标注 去 100% 还原 CSS 动画 ;
  • 学会使用常用的 前端动画开源库 。

任务目的

  • 熟悉 CSS transform 各项子属性
  • 理解 CSS transform 2D 变形

任务描述

通过 CSS transform 实现如 设计图 中所示效果，要求达到对设计稿的百分百的还原。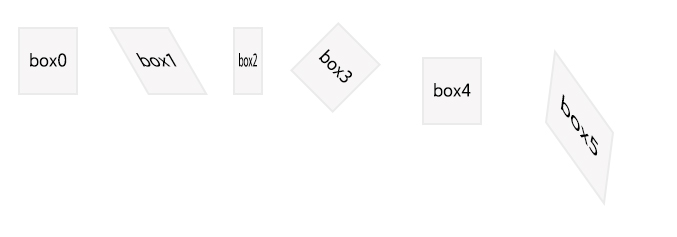
img

下载设计图源文件

  • 其中，你应当实现的变换效果已经在 Psd 中标明
    img

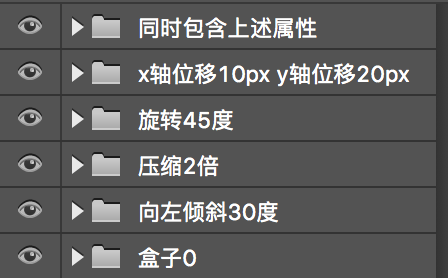
任务注意事项

  • 注意不同浏览器中的兼容性
  • 请注意代码风格的整齐、优雅
  • HTML 及 CSS 代码结构清晰、规范
  • 代码中含有必要的注释

分析

CSS transforms allows elements styled with CSS to be transformed in two-dimensional space. This specification is the convergence of the CSS 2D transforms and SVG transforms specifications.

补白

在css2d转换中，常见于如下 2D 转换方法：

  • skew()

    通过 skew() 方法，元素翻转给定的角度，根据给定的水平线（X 轴）和垂直线（Y 轴）参数： 

1
2
3
4
5
6
7
.box1{
            transform: skew(30deg,0deg);
            -ms-transform: skew(30deg,0deg);	/* IE 9 */
            -webkit-transform: skew(30deg,0deg);	/* Safari and Chrome */
            -o-transform: skew(30deg,0deg);	/* Opera */
            -moz-transform: skew(30deg,0deg);	/* Firefox */
}

  • scale()

    x,y轴的放大角度

1
2
3
4
5
6
7
.box2{
            transform: scale(0.5,1);
            -ms-transform: scale(0.5,1);	/* IE 9 */
            -webkit-transform: scale(0.5,1);	/* Safari 和 Chrome */
            -o-transform: scale(0.5,1);	/* Opera */
            -moz-transform: scale(0.5,1);	/* Firefox */
}

  • rotate()

    旋转角度

1
2
3
4
5
6
7
.box3{
            transform: rotate(45deg);
            -ms-transform: rotate(45deg);		/* IE 9 */
            -webkit-transform: rotate(45deg);	/* Safari and Chrome */
            -o-transform: rotate(45deg);		/* Opera */
            -moz-transform: rotate(45deg);		/* Firefox */
}

  • translate()

    通过 translate() 方法，元素从其当前位置移动，根据给定的 left（x 坐标） 和 top（y 坐标） 位置参数：

1
2
3
4
5
6
7
.box4{
            transform: translate(10px,20px);
            -ms-transform: translate(10px,20px);		/* IE 9 */
            -webkit-transform: translate(10px,20px);	/* Safari and Chrome */
            -o-transform: translate(10px,20px);		/* Opera */
            -moz-transform: translate(10px,20px);		/* Firefox */
        }

详解matrix() 方法

把所有 2D 转换方法组合在一起。

matrix() 方法需要六个参数，包含数学函数，允许您：旋转、缩放、移动以及倾斜元素。

matrix()中的6个参数代表了一个3*3的矩阵（线性代数）。

平移

在CSS3中我们矩阵的原始值是这样的

transforms:matrix(1,0,0,1,0,0);

写成我们数学里矩阵的形式是这样的

img

这么看起来，我们不太好分辨哪个数字对应的是我们上面写的matrix值里的哪一个，那为了便于描述我们把它写成：

transforms:matrix(a,b,c,d,e,f);

那么写成数学矩阵式就是这样的：

img

根据我们上面说的用矩阵与向量的乘法来施加运动，我们就可以来看一下它到底是怎么运动起来的

img

这么一来我们可以得到一个式子就是：

x’=ax+cy+e

y’=bx+dy+f

x’和y’就是我们变换后的水平位置坐标和垂直位置坐标，现在我们想要把元素往x轴的正方向平移10，在y轴方向上不动,反映到方程式里，我们要怎么来实现呢

元素往x轴的正方形平移10，在y轴方向上不动，反映到方程式里：

x’=ax+cy+e —（x’=ax+cy+e+10)

y’=bx+dy+f （不变）

元素往y轴的正方向平移10，在x轴方向上不动，反映到方程式里：

x’=ax+cy+e （不变）

y’=bx+dy+f —（y’=bx+dy+f+10）

元素同时往x轴正向和y轴正向移动10个单位 ：

我们用css矩阵来写：transform： matrix（1,0,0,1,10,10）–其他数值都不动，e和f分别加10

结论：平移只有跟e和f有关系，跟其他a,b,c,d没有关系，它们该怎么样还是怎么样，e对应x轴的平移，f对应y轴的平移，往正方向平移多少单位就加上多少单位，反之则减去多少个单位。

缩放

平移就是x或者y加减一个常数来得到的，理解了平移之后缩放就很简单了，可不就是x和y的倍数发生了变化么，反映到式子上来那就是系数的变化，那同样道理我们把上面的式子拿过来

x放大2倍 y不变

x’=ax+cy+e—（x’=2ax+cy+e) 就是x的系数增大2倍

y’=bx+dy+f (不变)

y放大2倍 x不变

x’=ax+cy+e (不变)

y’=bx+dy+f—(y’=bx+2dy+f)

就是y的系数增大2倍x和y都放大2倍，就是x和y的系数都增大2倍写成矩阵就是：

transform：matrix（2,0,0,2,0,0)

结论：缩放只有跟a和b有关系，跟其他数值都无关，a对应x轴缩放，b对应y轴缩放，缩放多少倍就乘以多少

旋转

相比于平移和缩放，旋转相对来说要复杂点了，当然搞清楚了就没什么难的了

transform：matrix（cosθ，-sinθ,sinθ,cosθ,0,0);

img

现在我们要让这个元素往顺时针方向旋转45°（sin45°=0.707，cos45°=0.707），那么我们给div加样式如下：

transform: matrix(0.707,0.707,-0.707,0.707,0,0);

img

这个div是不是就按我们预期的一样往顺时针方向转了45°了；

接下来我们把这个旋转放到数学里来看下
那同样的我们把它写成数学里矩阵的形式：

img

同样的根据矩阵的计算公式，我们可以得到公式：

x’=xcosθ-ysinθ; y’=xsinθ+ycosθ

现在我们先把公式放在这里，我们来看一下下图的这个正方形，从图中我们可以知道a,b,c,d的坐标分别为：

A(0,1) B(1,1) C(1,0) D(0,0)

当我们让它旋转90°之后，那此时的cos45°就是0 sin45°都为1，分别把A,B,C,D里的x,y代入上面的公式之后我们可以得到：

现在这个正方形就变成了下图的样子，和我们写代码达到的效果是一样的：

img

结论：我们要记住初始写法是这样的
transform：matrix（cosθ，-sinθ,sinθ,cosθ,0,0);然后需要旋转多少度就计算出这个度数的cosθ，sinθ就可以达到想要的效果。

参考资料